What is a computer?
A computer system an electronic machine that can be used to carry out specific instructions over and over or programmed to carry out a set of instructions.
Computers can perform calculations and logical operations very quickly, thousands of times faster than a human being. However, it's important to note that computer systems are not intelligent and cannot think for themselves - they rely on humans to program them.
A computer program is a series of instructions that are run on a computer system, Charles Babbage and Ada Lovelace are often considered the first people to create a computer program that could be run on a digital machine. This machine was called the Analytical Engine.
Computer basics
Computer systems are built using physical hardware. Hardware is the tangible parts of a computer. This hardware is able to run software. These days software is programmed to carry out millions of instructions and be able to provide many operations. The software that runs on the computer system can be changed very easily, so computers aren't limited to run specific programs.
Computer software and hardware communicate through a special type of software known as firmware.
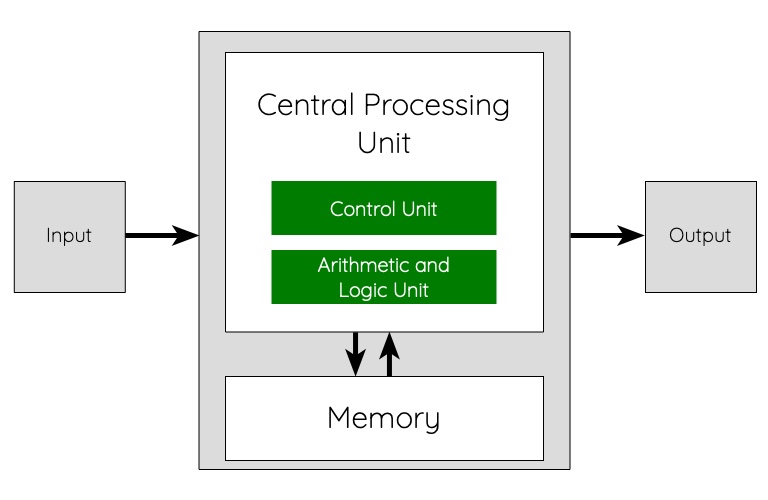
Modern computer systems follow an architecture or model called the von Neumann architecture developed by mathematician John von Neumann. Simply put, this describes how all computer systems operate.
The von Neumann architecture describes a computer system. It consists of a central processing unit or CPU which can decode and execute instructions. The CPU should be also be able to read instructions directly from some kind of memory. It should also be able to store data in memory as well.
In the von Neumann architecture at least, the term memory refers to both temporary and permanent memory, but generally speaking memory refers only to temporary memory whereas backing storage refers to the storage used to permanently store data.
The von Neumann architecture describes the operation of a computer system as a machine that receives an input performs some process on it and provides an output. Computer systems can therefore be perceived as a mathematical function. For example take function, f which has some domain X and a codomain of Y, this could be shown as:
$$f: X \to Y$$
Given some input, the same output should occur each time. If this was not the case, computers would be utterly useless since the result would be inconsistent.
Semiconductors
The invention of the semiconductor is one of the most fundamental reasons we have digital computers today.
A semiconductor is neither a perfect electrical conductor nor a perfect electrical insulator and it's electrical resistance drops based on certain variables or conditions such as the temperature of the semiconductor.
Semiconductors are generally made from either silicon or germanium. To make them acts in different ways, they are given impurities by a process called doping. Generally, these impurities are added to increase conductivity and is done by adding an element such as arsenic.
Semiconductors have many uses, but from the point of view of computer systems, the most common use is for constructing transistors.
A transistor is a special kind of semiconductor that acts like a switch. It has three terminals: two inputs and one output. Input one is a basic voltage that is passed through an open switch. The second input is used to determine whether to open the switch or not. Several types of transistors open at 0.7 volts but others are lower or higher than this. Finally, the third terminal is the output which is 0 or the input.
Binary
Since computer systems work with transistors, which are essentially switches, combining these switches together allows a computer to represent many different values.
Encoding using transistors is called binary and is the way in which computer systems represent values.
Binary works with two numbers, 0 and 1, therefore it is often refered to as base 2.
There is more in this tutorial in a later article about binary calculations.
Logic
Since transistors can be combined, it is also possible to combine transistors to make logic representable by computers. This allows computers to perform decision making, mathematical operations and operate on values.
The combinations of transistors into groups allows the creation of logic gates.
There are several gates that computer systems use:
- NOT gate
- AND gate
- OR gate
- XOR gate
- NAND gate
- NOR gate
- XNOR gate
Logic like this can be represented using truth tables which describe the result of the inputs of a gate.
There is more in the Conditions article of the Programming Theory course on this website.
NOT
The third type of gate is the NOT gate. This kind of gate only takes one input, which is negates it's input value. This basically means if it is given an input of true, the output becomes false and if given an input of false the output becomes true.
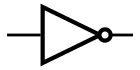
ANSI NOT gate symbol
NOT is also known as logical negation.
NOT gates are often combined with other gates, such as AND, OR and XOR, to make other gates called NAND, NOR and XNOR respectively.
In propositional logic the ¬ symbol is used to represent NOT.
Below is the truth table for NOT:
| A | ¬A |
|---|---|
| TRUE | FALSE |
| FALSE | TRUE |
AND
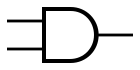
ANSI AND gate symbol
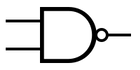
ANSI NAND gate symbol
An AND gate works on two inputs. It returns true when precisely both inputs are true. That is, it is false unless both inputs are true. By combining an AND gate with a NOT gate, we can get a NAND gate. NAND returns true whenever one or both inputs are false.
AND is also known as logical conjunction.
In propositional logic, AND is represented by the ∧ symbol whereas NAND is represented by ↑.
Below is a truth table for AND and NAND:
| A | B | A ∧ B | A ↑ B |
|---|---|---|---|
| TRUE | TRUE | TRUE | FALSE |
| TRUE | FALSE | FALSE | TRUE |
| FALSE | TRUE | FALSE | TRUE |
| FALSE | FALSE | FALSE | TRUE |
OR
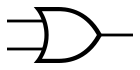
ANSI OR gate symbol
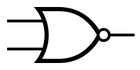
ANSI NOR gate symbol
Another type of gate is the OR gate. OR also takes two inputs but is true when both inputs are true or one of the inputs is true. By combining an OR gate with a NOT gate, we can get a NOR gate. NOR returns true only when both inputs are false.
OR is also known as logical disjunction.
In propositional logic OR is represented by the ∨ symbol whereas NOR is represented by ↓.
Below is the truth table for OR and NOR:
| A | B | A ∨ B | A ↓ B |
|---|---|---|---|
| TRUE | TRUE | TRUE | FALSE |
| TRUE | FALSE | TRUE | FALSE |
| FALSE | TRUE | TRUE | FALSE |
| FALSE | FALSE | FALSE | TRUE |
XOR
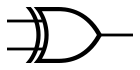
ANSI XOR gate symbol
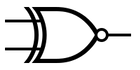
ANSI XNOR gate symbol
XOR is a special kind of logic gate. It also accepts two inputs and is similar to OR. XOR is true only when one input is true, but not when both are true. XNOR is different in that is true when both inputs are the same.
This can be represented as ¬(A ∧ B) ∧ (A ∨ B).
XOR is short for exclusive or.
In propositional logic XOR is represented by the ⊕ symbol whereas XNOR is simply ¬(A ⊕ B).
Below is the truth table for XOR and XNOR:
| A | B | A ⊕ B | ¬(A ⊕ B) |
|---|---|---|---|
| TRUE | TRUE | FALSE | TRUE |
| TRUE | FALSE | TRUE | FALSE |
| FALSE | TRUE | TRUE | FALSE |
| FALSE | FALSE | FALSE | TRUE |
For each of the following propositional logic statements, state whether it is true or false when A = TRUE and B = FALSE:
- A ∧ B
- FALSE
- A ∨ B ∧ B
- TRUE
- (A ∨ B) ∧ B
- FALSE
- (A ∧ B) ⊕ B
- FALSE
- ¬(A ∧ B) ⊕ B
- TRUE
- ¬(¬(A ∧ B) ⊕ B) ∨ (A ∧ ¬B)
- TRUE